YeoJohnsonTransformer#
The YeoJohnsonTransformer() applies the Yeo-Johnson transformation to the numerical variables.
The Yeo-Johnson transformation is defined as:
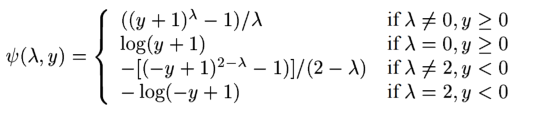
where Y is the response variable and λ is the transformation parameter.
The Yeo-Johnson transformation implemented by this transformer is that of SciPy.stats.
Example
Let’s load the house prices dataset and separate it into train and test sets (more details about the dataset here).
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from feature_engine import transformation as vt
# Load dataset
data = data = pd.read_csv('houseprice.csv')
# Separate into train and test sets
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['Id', 'SalePrice'], axis=1),
data['SalePrice'], test_size=0.3, random_state=0)
Now we apply the Yeo-Johnson transformation to the 2 indicated variables:
# set up the variable transformer
tf = vt.YeoJohnsonTransformer(variables = ['LotArea', 'GrLivArea'])
# fit the transformer
tf.fit(X_train)
With fit(), the YeoJohnsonTransformer() learns the optimal lambda for the transformation.
Now we can go ahead and trasnform the data:
# transform the data
train_t= tf.transform(X_train)
test_t= tf.transform(X_test)
Next, we make a histogram of the original variable distribution:
# un-transformed variable
X_train['LotArea'].hist(bins=50)
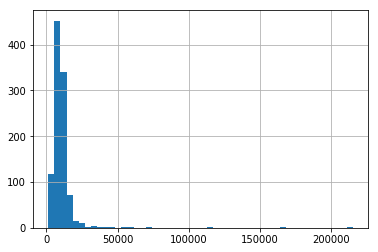
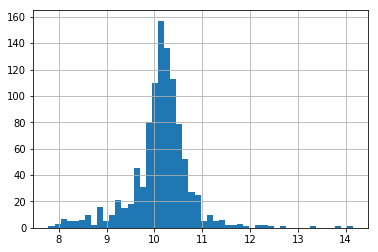
And now, we can explore the distribution of the variable after the transformation:
# transformed variable
train_t['LotArea'].hist(bins=50)
More details#
You can find more details about the YeoJohnsonTransformer() here:
For more details about this and other feature engineering methods check out these resources:
Feature engineering for machine learning, online course.
