LogTransformer#
The log transformation is used to transform skewed data so that the values are more evenly distributed across the value range.
Some regression models, like linear regression, t-test and ANOVA, make assumptions about the data. When the assumptions are not met, we can’t trust the results. Applying data transformations is common practice during regression analysis because it can help make the data meet those assumptions and hence obtain more reliable results.
The logarithm function is helpful for dealing with positive data with a right-skewed distribution. That is, those variables whose observations accumulate towards lower values. A common example is the variable income, with a heavy accumulation of values toward lower salaries.
More generally, when data follows a log-normal distribution, then its log-transformed version approximates a normal distribution.
Other useful transformations are the square root transformation, power transformations and the box cox transformation.
In statistical analysis, we can apply the logarithmic transformation to both the dependent variable (that is, the target) and the independent variables (that is, the predictors). These can help meet the linear regression model assumptions and unmask a linear relationship between predictors and response variable.
With Feature-engine, we can only log transform input features. You can easily transform the target variable by applying np.log(y).
The LogTransformer#
The LogTransformer() applies the natural logarithm or the logarithm in base 10 to numerical variables. Note that the logarithm can only be applied to positive values. Thus, if the variable contains 0 or negative variables, this transformer will return and error.
To transform non-positive variables you can add a constant to shift the data points towards positive values. You can do this from within the transformer by using LogCpTransformer().
Python implementation#
In this section, we will apply the logarithmic transformation to some independent variables from the Ames house prices dataset.
Let’s start by importing the required libraries and transformers for data analysis and then load the dataset and separate it into train and test sets.
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from feature_engine.transformation import LogTransformer
data = fetch_openml(name='house_prices', as_frame=True)
data = data.frame
X = data.drop(['SalePrice', 'Id'], axis=1)
y = data['SalePrice']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)
print(X_train.head())
In the following output we see the predictor variables of the house prices dataset:
MSSubClass MSZoning LotFrontage LotArea Street Alley LotShape \
254 20 RL 70.0 8400 Pave NaN Reg
1066 60 RL 59.0 7837 Pave NaN IR1
638 30 RL 67.0 8777 Pave NaN Reg
799 50 RL 60.0 7200 Pave NaN Reg
380 50 RL 50.0 5000 Pave Pave Reg
LandContour Utilities LotConfig ... ScreenPorch PoolArea PoolQC Fence \
254 Lvl AllPub Inside ... 0 0 NaN NaN
1066 Lvl AllPub Inside ... 0 0 NaN NaN
638 Lvl AllPub Inside ... 0 0 NaN MnPrv
799 Lvl AllPub Corner ... 0 0 NaN MnPrv
380 Lvl AllPub Inside ... 0 0 NaN NaN
MiscFeature MiscVal MoSold YrSold SaleType SaleCondition
254 NaN 0 6 2010 WD Normal
1066 NaN 0 5 2009 WD Normal
638 NaN 0 5 2008 WD Normal
799 NaN 0 6 2007 WD Normal
380 NaN 0 5 2010 WD Normal
[5 rows x 79 columns]
Let’s inspect the distribution of 2 variables from the original data with histograms.
X_train[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()
In the following plots we see that the variables show a right-skewed distribution, so they are good candidates for the log transformation:
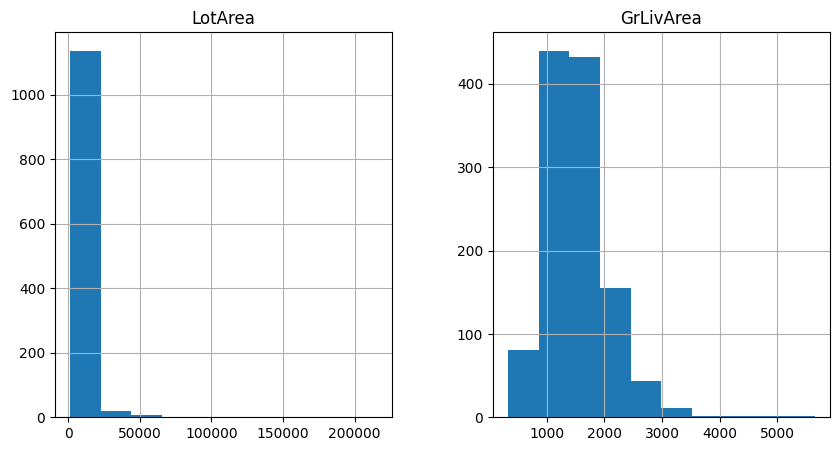
We want to apply the natural logarithm to these 2 variables in the dataset using the
LogTransformer(). We set up the transformer as follows:
logt = LogTransformer(variables = ['LotArea', 'GrLivArea'])
logt.fit(X_train)
With fit(), this transformer does not learn any parameters, but it checks that the variables you entered are numerical, or if no variable was entered, it will automatically find all numerical variables.
To apply the logarithm in base 10, pass '10' to the base parameter when setting up the transformer.
Now, we can go ahead and transform the data:
train_t = logt.transform(X_train)
test_t = logt.transform(X_test)
Let’s now examine the variable distribution in the log-transformed data with histograms:
train_t[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()
In the following histograms we see that the natural log transformation helped make the variables better approximate a normal distribution.
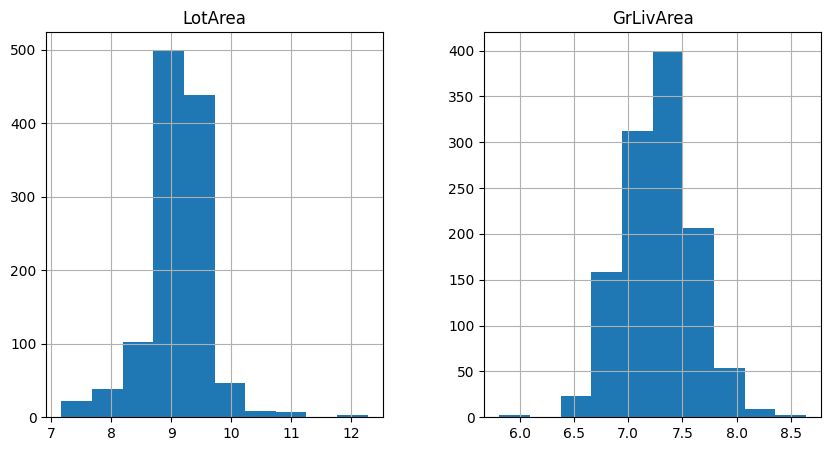
Note that the transformed variable has a more Gaussian looking distribution.
If we want to recover the original data representation, with the method inverse_transform, the LogTransformer() will apply the exponential function to obtain the variable in its original scale:
train_unt = logt.inverse_transform(train_t)
test_unt = logt.inverse_transform(test_t)
train_unt[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()
In the following plots we see histograms showing the variables in their original scale:

Following the transformations with scatter plots and residual analysis of the regression models helps understand if the transformations are useful in our regression analysis.
Tutorials, books and courses#
You can find more details about the LogTransformer() here:
For tutorials about this and other data transformation methods, like the square root transformation, power transformations, the box cox transformation, check out our online course:

Feature Engineering for Machine Learning#
Or read our book:

Python Feature Engineering Cookbook#
Both our book and course are suitable for beginners and more advanced data scientists alike. By purchasing them you are supporting Sole, the main developer of Feature-engine.
