ReciprocalTransformer#
The ReciprocalTransformer() applies the reciprocal transformation 1 / x to
numerical variables.
The ReciprocalTransformer() only works with numerical variables with non-zero
values. If a variable contains the value 0, the transformer will raise an error.
Let’s load the house prices dataset and separate it into train and test sets (more details about the dataset here).
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from feature_engine import transformation as vt
# Load dataset
data = data = pd.read_csv('houseprice.csv')
# Separate into train and test sets
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['Id', 'SalePrice'], axis=1),
data['SalePrice'], test_size=0.3, random_state=0)
Now we want to apply the reciprocal transformation to 2 variables in the dataframe:
# set up the variable transformer
tf = vt.ReciprocalTransformer(variables = ['LotArea', 'GrLivArea'])
# fit the transformer
tf.fit(X_train)
The transformer does not learn any parameters. So we can go ahead and transform the variables:
# transform the data
train_t= tf.transform(X_train)
test_t= tf.transform(X_test)
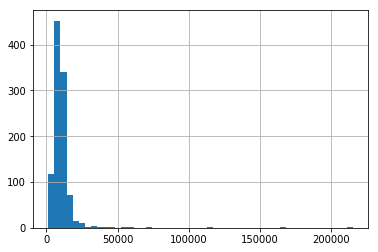
Finally, we can plot the original variable distribution:
# un-transformed variable
X_train['LotArea'].hist(bins=50)
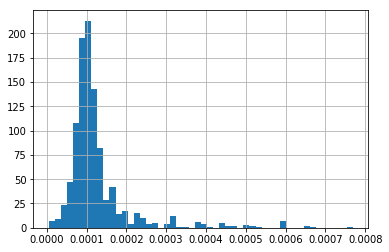
And now the distribution after the transformation:
# transformed variable
train_t['LotArea'].hist(bins=50)
More details#
You can find more details about the ReciprocalTransformer() here:
For more details about this and other feature engineering methods check out these resources:
Feature engineering for machine learning, online course.
