EqualWidthDiscretiser#
The EqualWidthDiscretiser() sorts the variable values into contiguous intervals
of equal size. The size of the interval is calculated as:
( max(X) - min(X) ) / bins
where bins, which is the number of intervals, should be determined by the user. The
interval limits are determined using pandas.cut().
A note on number of intervals
Common values are 5 and 10. Note that if the variable is highly skewed or not continuous smaller intervals maybe required. Otherwise, the transformer will introduce np.nan.
The EqualWidthDiscretiser() works only with numerical variables. A list of
variables to discretise can be indicated, or the discretiser will automatically select
all numerical variables in the train set.
Example
Let’s look at an example using the House Prices Dataset (more details about the dataset here).
Let’s load the house prices dataset and separate it into train and test sets:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from feature_engine.discretisation import EqualWidthDiscretiser
# Load dataset
data = data = pd.read_csv('houseprice.csv')
# Separate into train and test sets
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['Id', 'SalePrice'], axis=1),
data['SalePrice'], test_size=0.3, random_state=0)
Now we want to discretise the 2 variables indicated below into 10 intervals of equal width:
# set up the discretisation transformer
disc = EqualWidthDiscretiser(bins=10, variables=['LotArea', 'GrLivArea'])
# fit the transformer
disc.fit(X_train)
With fit() the transformer learns the boundaries of each interval. Then, we can go
ahead and sort the values into the intervals:
# transform the data
train_t= disc.transform(X_train)
test_t= disc.transform(X_test)
The binner_dict_ stores the interval limits identified for each variable.
disc.binner_dict_
'LotArea': [-inf,
22694.5,
44089.0,
65483.5,
86878.0,
108272.5,
129667.0,
151061.5,
172456.0,
193850.5,
inf],
'GrLivArea': [-inf,
768.2,
1202.4,
1636.6,
2070.8,
2505.0,
2939.2,
3373.4,
3807.6,
4241.799999999999,
inf]}
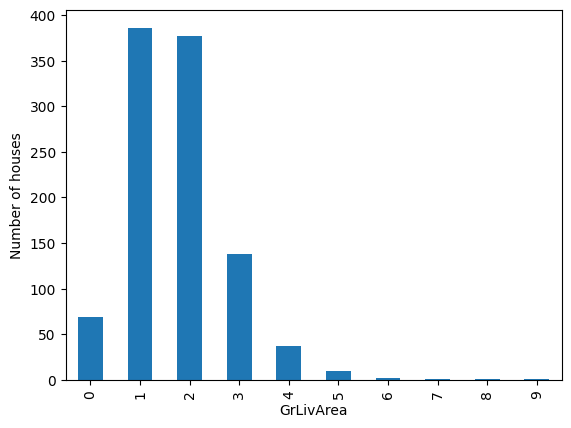
With equal width discretisation, each bin does not necessarily contain the same number of observations.
train_t.groupby('GrLivArea')['GrLivArea'].count().plot.bar()
plt.ylabel('Number of houses')
We can see below that the intervals contain different number of observations.
Discretisation plus encoding
If we return the interval values as integers, the discretiser has the option to return the transformed variable as integer or as object. Why would we want the transformed variables as object?
Categorical encoders in Feature-engine are designed to work with variables of type
object by default. Thus, if you wish to encode the returned bins further, say to try and
obtain monotonic relationships between the variable and the target, you can do so
seamlessly by setting return_object to True. You can find an example of how to use
this functionality here.
Additional resources#
Check also for more details on how to use this transformer:
For more details about this and other feature engineering methods check out these resources:

Feature Engineering for Machine Learning#
Or read our book:

Python Feature Engineering Cookbook#
Both our book and course are suitable for beginners and more advanced data scientists alike. By purchasing them you are supporting Sole, the main developer of Feature-engine.
